CONCLUSIÓN

Este portafolio se realizo con el fin de los alumnos que están estudiando gastronomías y próximos a estudiar entiendan la importancias de las matemática en nuestra división, son de suma importancias, ya que con estas podemos sacar costos, convertir medidas, ver la demanda de los platillos a través de la estadística y ademas que hay muchos jóvenes que piensan que la gastronomía no lleva matemáticas y al cursar la carrera hay deserción por no entender la materia y con esto pueden conocer mas a fondo la carrera.

PROYECTO

Llevando a cabo el tema de estadística realizamos una encuesta a 100 personas con el tema de Alimentos y Bebidas, preguntando cuales eran sus gustos.

Aquí te dejo el link. 

ESTADÍSTICA

La Estadística trata del recuento, ordenación y clasificación de los datos obtenidos por las observaciones, para poder hacer comparaciones y sacar conclusiones.

Un estudio estadístico consta de las siguientes fases:

• Recogida de datos.
• Organización y representación de datos.
• Análisis de datos.
• Obtención de conclusiones

Trabajo realizado 

CONCEPTOS BÁSICOS:

Población

Una población es el conjunto de todos los elementos a los que se somete a un estudio estadístico.

Individuo

Un individuo o unidad estadística es cada uno de los elementos que componen la población.

Muestra

Una muestra es un conjunto representativo de la población de referencia, el número de individuos de una muestra es menor que el de la población.

Muestreo

El muestreo es la reunión de datos que se desea estudiar, obtenidos de una proporción reducida y representativa de la población.

Valor

Un valor es cada uno de los distintos resultados que se pueden obtener en un estudio estadístico. Si lanzamos una moneda al aire 5 veces obtenemos dos valores: cara y cruz.

Dato

Un dato es cada uno de los valores que se ha obtenido al realizar un estudio estadístico. Si lanzamos una moneda al aire 5 veces obtenemos 5 datos: cara, cara, cruz, cara, cruz.

Ejercicios

Como ejercicio de Proporción Directa e Inversa realizamos costeo de eventos para un determinado numero de personas al igual que utilizamos todas las herramientas aprendidas anteriormente por el profesor ya que esto nos ayudara a poder costear el precio de cualquier producto que vallamos a vender y así no tener perdidas económicas si no tener un precio adecuado para el cliente.

QUEBRADOS

La forma más accesible de comprender el concepto del "quebrado" como elemento aritmético, es la referencia a las fracciones más corrientemente mencionadas; tales como "la mitad", "un tercio", "un cuarto". En estas expresiones, se está significando que la unidad ha sido dividida en dos, tres o cuatro partes iguales, de las cuales se toma en consideración solamente una. Aunque igualmente es posible hacerlo con más de una (dos tercios) y también es posible considerar que esas fracciones en su conjunto superen una unidad, como cuando se consideran "cinco tercios", por ejemplo, que equivalen por lo tanto a una unidad más dos tercios de otra.

Leer mas aqui

MCD Y MCM

MÁXIMO COMÚN DIVISOR:

El Máximo Común Divisor es, como su nombre indica, el mayor de los divisores comunes de varios números. Para calcularlo, se descompone cada uno de ellos en factores primos. El M.C.D. es el resultado de multiplicar los factores que se repitan en todas las descomposiciones, afectados por el menor exponente.
En el caso de que no se repita ningún factor, el M.C.D. de esos números es 1, y se dice que los números son “primos entre sí”. Por ejemplo, el 18 y el 25 son primos entre sí.

MÍNIMO COMÚN MÚLTIPLO:

El Mínimo Común Múltiplo es, así mismo, el menor de los múltiplos comunes a varios números. Para calcularlo, descomponemos los números en factores primos, y el M.C.M es el resultado de multiplicar los factores comunes y los no comunes, afectados por el mayor exponente.
Si los números son primos entre sí, el M.C.M. es el producto entre ellos.

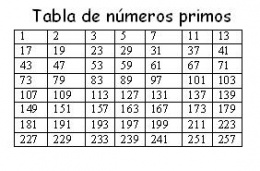
NÚMEROS PRIMOS

  Un número primo es un número entero mayor que cero, que tiene exactamente dos divisores positivos. También podemos definirlo como aquel número entero positivo que no puede expresarse como producto de dos números enteros positivos más pequeños que él, o bien, como producto de dos enteros positivos de más de una forma. Conviene observar que con cualquiera de las dos definiciones el 1 queda excluido del conjunto de los números primos.
 Ejemplos: a) El 7 es primo. Sus únicos divisores son 1 y 7. Sólo puede expresarse como producto de 7·1.
                       b) El 15 no es primo. Sus divisores son 1, 3, 5 y 15. Puede expresarse como 3·5. (y también como 15·1)

Mas información AQUÍ

EJERCICIOS

Ejercicios realizados en el tema de conversiones utilizando las tablas de Equivalencia de Sistemas.  

EQUIVALENCIAS

Como lo mencionamos anteriormente, las matemáticas tienen una función muy importante en la cocina.
A continuación les mostrare algunos de los ejemplos que se trabajaron en la unidad de Matemáticas Aplicadas a la Gastronomía.
1. Equivalencias en el sistema Ingles, Métrico e Internacional.
Relación de igualdad en el valor de dos cosas o entidades.

Importancia de las matemáticas en la cocina.

Las personas que llevan a cabo exitosamente la operación de servicios de alimentación, comprenden lo necesario que son las matemáticas básicas para calcular adecuadamente los diversos requerimientos desde la propia elaboración de los productos hasta los costos de una comida por consumidor por ejemplo, y así poner precio a un menú.
Aquí les dejo un vídeo que demuestra la importancia de las matemáticas: 

MATEMÁTICAS

Aplicadas a la Gastronomía:

Si pones atención, te darás cuenta que las matemáticas están presentes en todo lo que realizas cuando preparas un platillo, postre o cualquier otro alimento, ya que de manera inmediata surgen, por ejemplo, las preguntas:” ¿Cuántas porciones necesito?”, “¿Qué cantidad de cada ingrediente es necesaria?”, “Cuánto tiempo lo dejo en el horno?”, como consecuencia “¿A qué temperatura?” y muchas otras como el caso de unidades de medición, los instrumentos a emplear e incluso, el contenido calórico o nutrimental.